betacode

История бит и байтов в информатике

  1. Bit
  2. Byte

1. Bit

Я начну рассказав сначала про десятичную систему, когда вы поймете про десятичную систему, наш разговор не будет прерван и непонятен.
OK, десятичная система является самой распространенной на данный момент, но она не единственная, много культур исползовали другие системы в прошлом, но в наше время почти все уже перешли на десятичную систему. Десятичная система использует цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, они соединяюются между собой, чтобы создать новое число.
Если у вас есть только одна ячейка, вы можете написать только цифру от 0 до 9. Но...
  • Если у вас есть 2 ячейки, вы можете написать число от 0 до 99.
  • Если у вас есть 3 ячейки, вы можете написать число от 0 до 999.
Ячейки справо налево имеют коэффициент, который поочередно является 10^0, 10^1, 10^2, ...
BIT
BIT является аббревиатурой Binary digIT (Единица информации). Один bit имеет значение 0 или 1, он называется наменьшей единицей в компьютере. 0, 1 это 2 базовых цифры 2-единичной системы.
Будем размышлять так словно десятичная система и она применяется к двуединичной системе, если у вас есть 1 ячейка, вы можете написать 2 цифры 0 и 1. Если у вас есть 2 ячейки, вы можете написать 4 числа 00, 01, 10, и 11 (Примечание: Не ошибайтесь, эти числа все являются числами двуединичной системы).
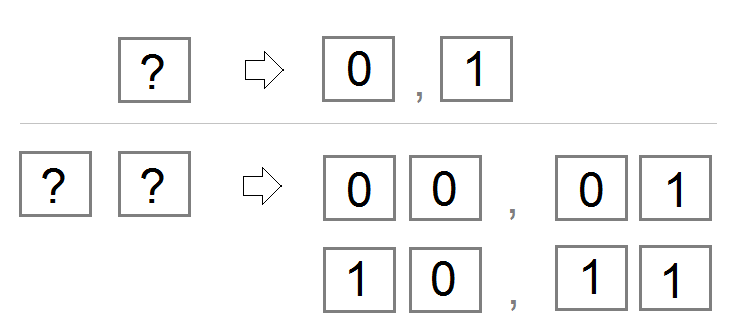
С двуединичной системой, ячейки справа налево имеют коэффициент, они поочередно являются 2^0, 2^1, 2^2, ...
В изображении наже описывается как конвертировать число в двуединичной системе на десятичную систему.
Таким образом:
  • Если у вас есть 2 ячейки в двуединичной системе, вы можете написать самое большое число это 11(2), оно эквивалентноо с числом 3 в десятичной системе.
  • NЕсли у вас есть 3 ячейки в двуединичной системе, вы можете написать самое большое число это 111(2), оно эквивалентноо с числом 7 в десятичной системе.
И у вас есть следующая таблица:
Box Numbers
Maximum Number (Base-2)
Convert to Base-10
1
1
1 (2^1 - 1)
2
11
3 (2^2 - 1)
3
111
7 (2^3 - 1)
4
1111
15 (2^4 - 1)
5
11111
31 (2^5 - 1)
6
111111
63 (2^6 - 1)
7
1111111
127 (2^7 - 1)
8
11111111
255 (2^8 - 1)
9
111111111
511 (2^9 - 1)
Почему компьютер использует двуединичную систему, а не десятичную?
Здесь вы точно зададите вопрос "Почему компьютер использует двуединичную систему? Почему не использует десятичную систему?". Раньше я так же задавался этим вопросом как и вы.
Компьютер работает используя миллионы электронных выключателей (electronic switches) (transistors - тразисторов), каждый transistor включен или выключен (похоже на выключатель лампочки, но намного меньше). Состояние переключения(включен или выключен) может представить бинарную информацию, например да или нет, верно или неверно, 1 или 0. Базовая единица информации в компьютере это двоичный символ (binary digit). Несмотря на то, что компьютер может представляет невероятное разнообразие информации, все представления в конце должны уменьшиться до статуса ON/OFF (включен/выключен) транзистора (transistor).
Поэтому ответом является то, что компьютер не имеет много статусов для хранения информации, таким образом он хранит информацию на основании двух состояний ON и OFF (Соответствует 1 и 0).
Жесткий диск вашего компьютера так же хранит информацию на основании принципа 0, 1. Жесткий диск включает рекордер и считыватель, имеет 1 или более дисков, эти диски покрыты никелевым слоем(magnetic layer of nikel), магнитные частицы (magnetic particle) могут иметь южно-северное или северо-южное направление, это 2 состояния магнитных частиц, и соответствует 0 и 1.
Считыватель жесткого диска может распознать направление магнитных частиц, чтобы конвертировать в сигналы 0 или 1.
Данные для хранения в жестком диске являются строкой сигналов 0 или 1. Рекордер на основании этих сигналов меняет соответственно направление магнитных частиц. Это и есть прицип хранения данных жесткого диска.

2. Byte

Byte это единица компьютера, она соответствует 8 bit. Таким образом, один byte может предтавить число в диапазоне от 0 до 255.
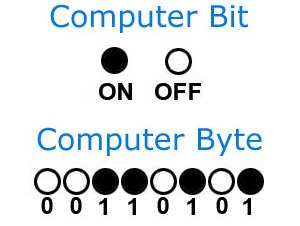
Почему 1 byte = 8 bit?
Теперь ваш вопрос это "Почему 1 byte = 8 bit, а не 10 bit?".
В начале компьютерной эпохи люди использовли baudot как базовую единицу, она соответствует 5 bit, значит нельзя представить числа от 0 до 31.Если каждое число представяет символ, то 32 хватает для прописных символов A, B, ... Z, и несколько других символов, ее не хватает для всех строчных символов.
Сразу после этого, некоторые компьютеры использовали 6 bit для представления символов, и она может представлять максимум 64 символов. Достаточно для A, B, .. Z, a, b.. Z, 0, 1, 2, .. 9. Но не хватает для других символов как +,-,*, / и символов пробелов. Так 6 bit быстро стала ограниченной.
ASCII уже определил набор символов 7-bit (7-bit character set). Это "достаточно хорошо" для многих использований за долгое время, и уже сформировал базу для почти всех самых новых символов это (ISO 646, ISO 8859, Unicode, ISO 10646, и т.д.)
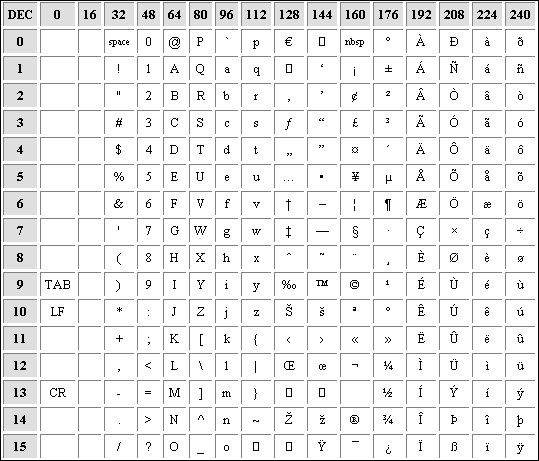
Таблица ASCII:
8-bit, немного больше по сравнению чем 7-bit будет лучше, он не создает большую трату. 8-bit это набор чисел от 0 до 255 и он удовлетворяет многих компьютерных дизайнеров, появилось понятие byte, 1 byte = 8 bit.
Для 8-bit, дизайнеры могут определить другие символы, включая особенные символы компьютера. Появилась таблица кода ANSI, которая является унаследованной от таблицы кода ASCII:
Таблица ANSI:
На данный момент существует много таблиц кода символов (character sets), которые появились с целью кодирования символов на разных языках. Например китайский, японский требуют много символов, в данном случае используется 2 byte, или 4 byte для определения символа.

Java Basic

Show More

Java Basic

Show More

Новейшие статьи

    Show More